Bonjour la Communauté !
Je voulais vous partager mes impressions du Meetup FHIR France #13, organisé par Fyrstain et sponsorisé par InterSystems – et franchement, c’était une soirée inoubliable ! C’était une soirée riche en échanges, en apprentissages et en belles rencontres !
L’accueil a débuté à 19h et @Guillaume Rongier a aidé à enregistrer les participants

Après avoir laissé les participants arriver tranquillement, nous avons officiellement lancé la soirée. Fanch Rouault a souhaité la bienvenue au nom de Fyrstain

Ensuite, Julie, l'organisatrice du group Communauté FHIR France, a pris la parole pour dire quelques mots

Puis @Guillaume Rongier a partagé une belle introduction sur FHIR et son impact croissant dans le domaine de la santé numérique

Ensuite, les présentations se sont enchaînées, chacune plus intéressante que la précédente :
« Comment les APIs FHIR du Serveur Multi-Terminologies (SMT) de l’ANS aident à gérer les artéfacts terminologiques de l’Europe » – par les gens d'Agence du Numérique en Santé


« Les avantages et gains de la plateforme FHIR du CHU de Toulouse : Des référentiels à l'architecture » – par CHU de Toulouse

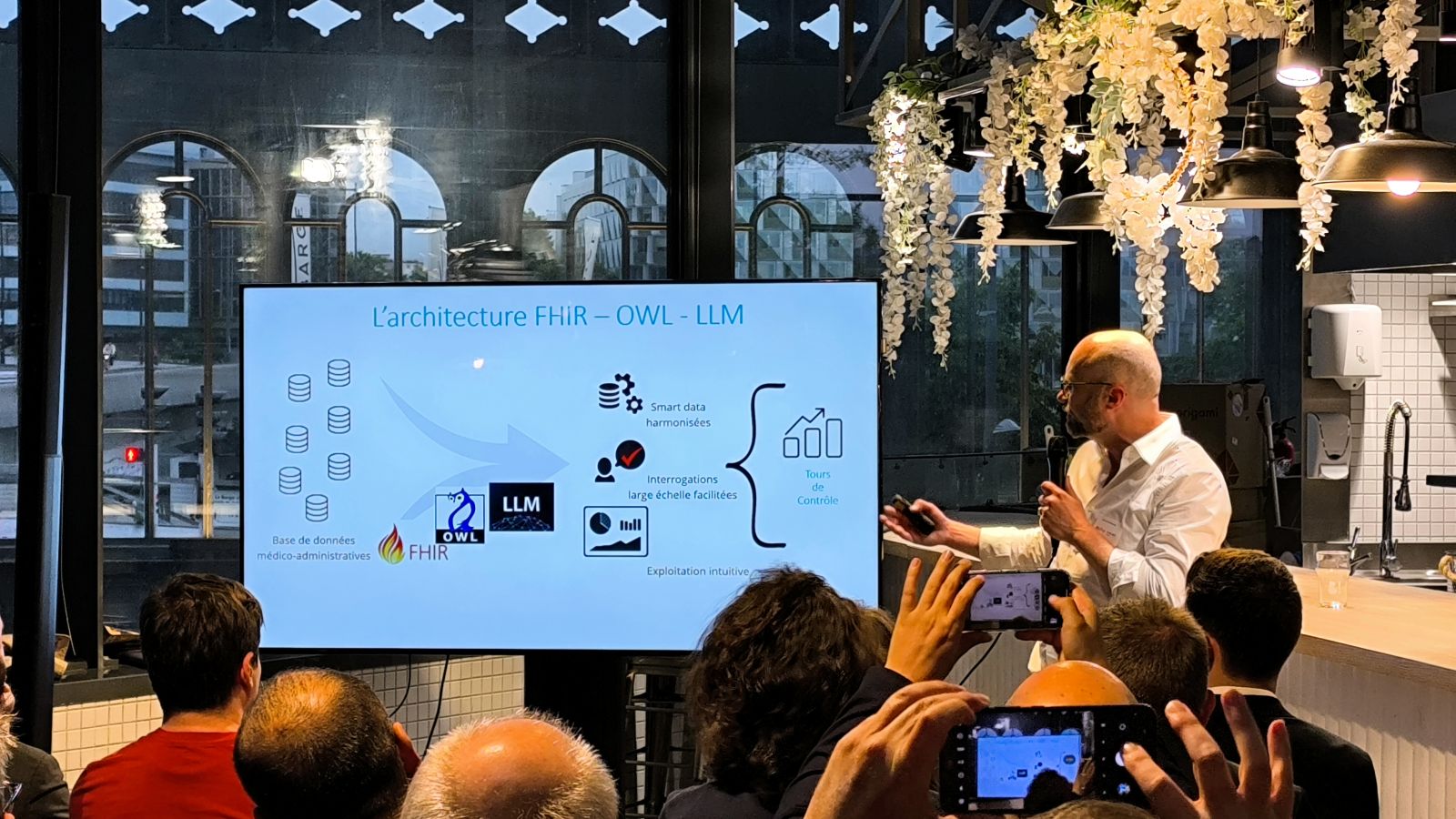
« Requêtage intelligent avec FHIR – OWL – LLM » – par @Yann de Cambourg de Synodis
« Prévoir et prévenir les urgences vitales grâce à HL7 FHIR » – par Quentin FRANCOIS de PREVIA MEDICAL

Après les présentations, nous avons terminé sur une note conviviale avec un cocktail et moment de networking – une super occasion pour échanger encore un peu autour d’un verre

Merci à tous les intervenants pour leurs interventions de qualité, aux participants pour leur présence et leur énergie, et à nos partenaires pour leur soutien.

( Fanch Rouault, @Adeline Icard et @Iryna Mykhailova )
Hâte de vous retrouver pour le prochain Meetup FHIR France !

.png)
.png)